DFS( Depth-First-Search) thuật toán DFS hay còn được gọi là thuật toán tìm kiếm theo chiều sâu và cấu trúc stack.

Có vô số cái tài liệu toán học hay lập trình có nội dung liên quan đến DFS hay depth first search nên ở bài này mình không đi vào chi tiết toán học hay đồ thị mà tập trung về sơ lược ý tưởng của DFS cũng như là các ứng dụng của DFS đối với các bài toán đồ thị khác và lý do tại sao DFS lại quan trọng đến như vậy.

1. Ý tưởng của DFS .

- DFS là một thuật toán thường xuyên được sử dụng đi hoặc tìm kiếm trong đồ thị và các Tree trong cấu trúc dữ liệu.

- DFS duyệt qua các đỉnh một lần duy nhất, không tính lần quay lại.

- DFS thường được thực hiện bằng đệ quy hoặc cấu trúc Stack. Riêng mình thấy cấu trúc Stack có hiệu quả hơn đệ quy dù không đáng kể vì trong một số trường hợp đặc biệt có thể dễ dàng quản lý các vị trí đã đi qua. Bản chất của cả hai đều là đi đến đích cuối cùng và quay lại.

Cấu trúc Stack :

 - Stack giống như một cái thùng để chứa sách. Lấy quyển nào bỏ vào thùng trước thì quyển đó sẽ được lấy ra cuối cùng, vì quyển sách đang nằm ở đáy thùng . Đó là bản chất của cấu trúc Stack.

Hình 1. Hình giống thùng tượng trưng cho stack và một dãy số liên kết.

Hình 2 . Lần lượt bỏ theo thứ tự 5,4,3,2,1 vào thùng.

Hình 3. Lần lượt lấy ra theo thứ tự 1,2,3,4,5 theo đúng thứ tự First In - Last Out.

Cấu trúc của đệ quy:

  - Đệ quy liên tiếp di chuyển trên đồ thị và cho đến khi tới được đích cuối cùng 

 thì bắt đầu quay đầu lại.

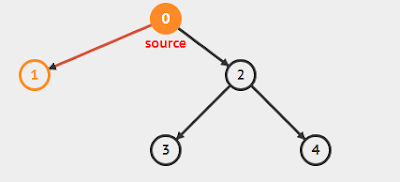
Ví dụ : đồ thị sau đây thể hiện cách DFS duyệt đỉnh trong đồ thị. 

*Lưu ý : DFS duyệt qua các đỉnh một lần duy nhất, không tính lần quay lại.

DFS bắt đầu đi từ đỉnh  0

Từ 0 đến 1

Từ 1 trở về 0

Từ 0 đến 2

Từ 2 đến 3

Từ 3 trở về 2

Từ  2 đến 4

Từ 4 trở về 2

Từ 2 trở về 0

Kết thúc quá trình duyệt.

2. Ứng dụng của DFS 

 - Vì tính chất duyệt qua mỗi đỉnh một lần, dfs có thể tìm ra chu trình trong đồ thì hoặc là xác định các tập đỉnh liên kết nhau, . . . Từ đó đi đến ứng dụng của các thuật toán cao cấp hơn .

  Một số ứng dụng.

1. Minimum Spaning Tree (MSP) : cây khung nhỏ nhất.

2. Detecting cycle in the graph: xác định chu trình trong đồ thị.

3. Path Finding: tìm đường đi giữa 2 đỉnh .

4. Topological Sorting: sort Topo.

5. Check Bipartite grapth : kiểm tra có phải đồ thị hai phía .

6. Finding Strongly component of a graph: tìm thành phần liên thông mạnh.

7.Maze solution : giải quyết các bài toán trong mê cung .

Do bài này đã dài nên các chủ đề trên sẽ được chia lại cho các phần sau.

khuy

Author & Editor

You may come here to learn not to laugh sorry bout that btw haha